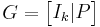Generator matrix
In coding theory, a generator matrix is a basis for a linear code, generating all its possible codewords. If the matrix is G and the linear code is C,
- w = cG
where w is a codeword of the linear code C, c is a row vector, and a bijection exists between w and c. A generator matrix for an ( ,
, 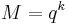 ,
,  )
) -code has dimensions k×n. Here n is the length of a codeword, k is the number of information bits, d is the minimum distance of the code, and q is the number of symbols in the alphabet (thus, q = 2 indicates a binary code, etc.). The number of redundant bits is denoted by r = n - k.
-code has dimensions k×n. Here n is the length of a codeword, k is the number of information bits, d is the minimum distance of the code, and q is the number of symbols in the alphabet (thus, q = 2 indicates a binary code, etc.). The number of redundant bits is denoted by r = n - k.
The systematic form for a generator matrix is
where 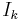 is a k×k identity matrix and P is of dimension k×r.
is a k×k identity matrix and P is of dimension k×r.
A generator matrix can be used to construct the parity check matrix for a code (and vice-versa).
Equivalent Codes
Codes C1 and C2 are equivalent (denoted C1 ~ C2) if one code can be created from the other via the following two transformations:
- permute components, and
- scale components.
Equivalent codes have the same distance.
The generator matrices of equivalent codes can be obtained from one another via the following transformations:
- permute rows
- scale rows
- add rows
- permute columns, and
- scale columns.